動機
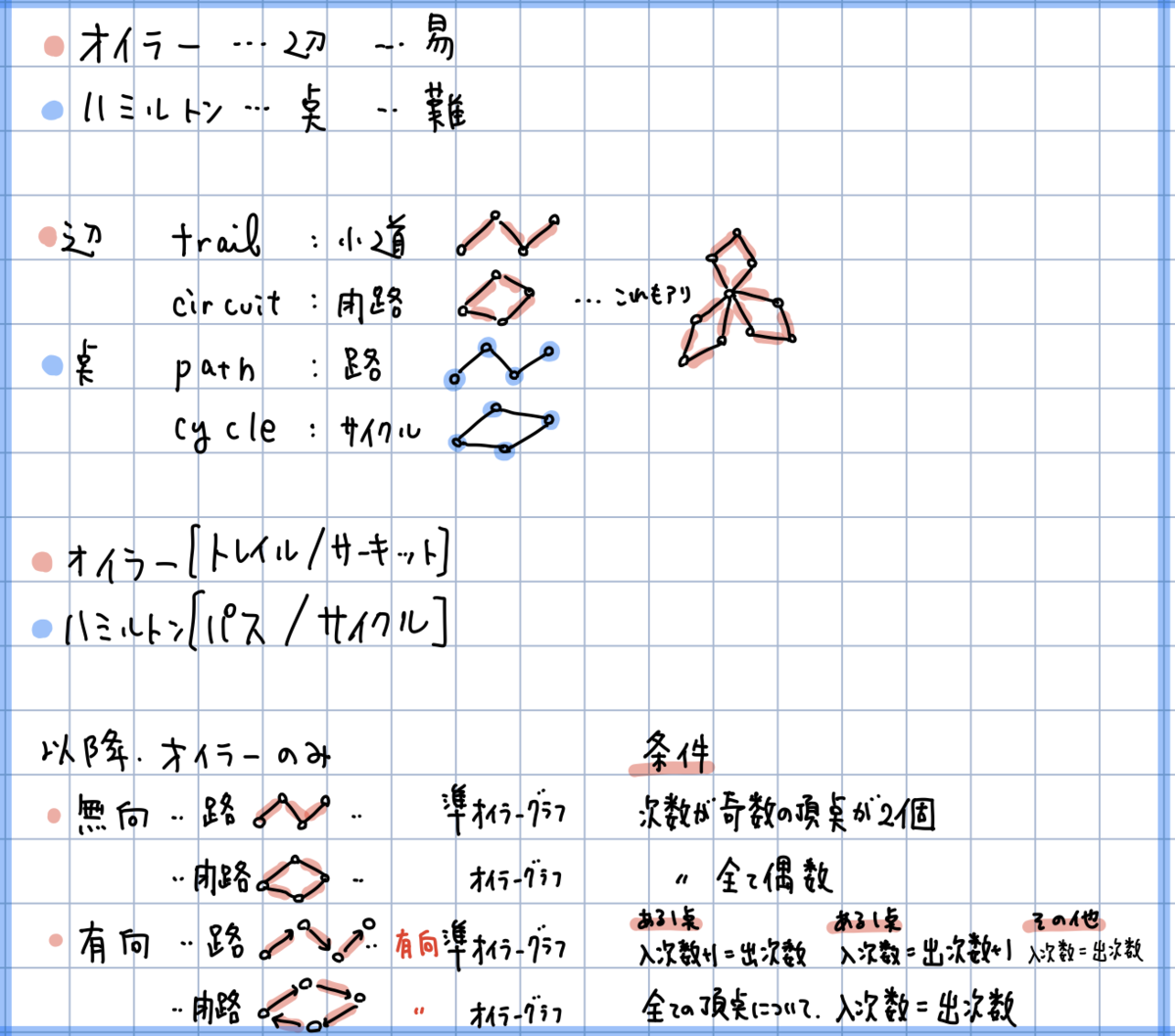
- trail, pathの違い、circuit, cycleの違いが曖昧で「オイラーパス」などという存在しない用語を発することがないようにまとめた
- 頂点に注目した時の用語が path, cycle
- 辺に注目した時の用語が trail, circuit
- なのでオイラー路 = Eulerian-Trail である
オイラー(閉)路の計算量
- (M : 辺数)
- 判定 O(M)
- 構築 O(M) https://ei1333.github.io/luzhiled/snippets/graph/eulerian-trail.html
参考
- Tech Tips: グラフ理論の紛らわしい言葉 http://techtipshoge.blogspot.com/2011/09/blog-post.html
- 競プロにおけるオイラー路とその応用について - Learning Algorithms https://kokiymgch.hatenablog.com/entry/2017/12/07/193238
- グラフ理論用語 英和対訳表 http://x-n.io/doc/graph-theory-terms
オイラー路の復元はdfsして帰りがけ順
オイラー路の復元をご存じない?
— ꑄ꒖ꐇꌅꏂ🐈 (@snuke_) June 4, 2020
dfsして帰りがけ順を取るとオイラー路になります。
- 具体例として4頂点の完全有向グラフのオイラー(閉)路を求めてみる
- 0を始点とし、まず0->0の辺を使い、次に0->1の辺を使い、1->0の辺を使い... という風に今まで使っていない辺を使ってdfsし、帰りがけ順に頂点を見るとオイラー(閉)路になっている
- 下記画像のように実際に書いて確認した

- コードとしての帰りがけ順は型があるようで、下記のように書く
- (https://codeforces.com/contest/1511/problem/D のeditorialより)
int n, k; int cur[26]; vector<int> path; void dfs(int v) { while (cur[v] < k) { int u = cur[v]++; dfs(u); path.push_back(u); // dfsしてからリストに足すのは「帰りがけ順」 } } int main() { scanf("%d%d", &n, &k); // k=4の場合 dfs(0); debug(path); // => {0, 3, 3, 2, 2, 3, 1, 2, 1, 1, 3, 0, 2, 0, 1, 0} printf("a"); for (int i = 0; i < n - 1; ++i) printf("%c", path[i % path.size()] + 'a'); printf("\n"); }
追記
- 辺を頂点とみてdfsしたと考えるほうが正しいか

オイラー(閉)路を使う問題
- shiritori - しりとり (Shiritori)
- https://atcoder.jp/contests/joisc2011/tasks/joisc2011_shiritori
- オイラー閉路なら1番小さい言葉を始点にする
- オイラー路なら始点は1つに決まる
- 復元は上の方法で