AOJ 2251 - Merry Christmas ～DAG上の最小パス被覆 minimum path cover～

• Quiz
  • http://judge.u-aizu.ac.jp/onlinejudge/description.jsp?id=2251
  • できるだけ少ないサンタでプレゼントを配る問題
• AC
  • http://judge.u-aizu.ac.jp/onlinejudge/review.jsp?rid=4866924#1
• 解説
  • L個の条件について、条件iを実行後、条件jに遷移できるなら辺をはる。これはDAGになる（場所じゃなくて条件を頂点にしている！）
  • そのDAG上の最小パス被覆が答え
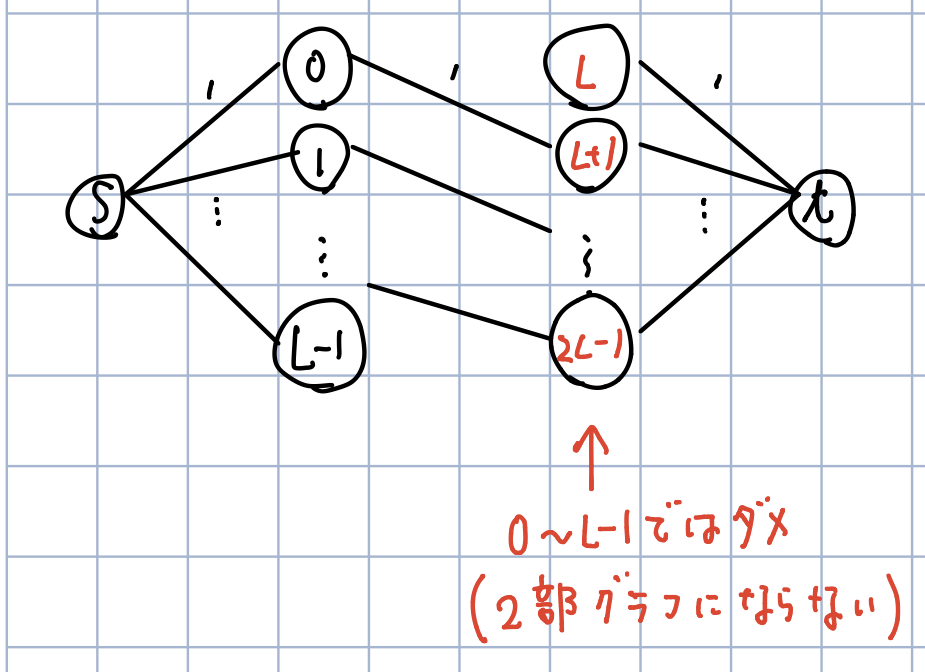
  • これは2部グラフのマッチングで解ける
• その他
  • 2部グラフのマッチングでフローを使うが、頂点を2倍にすることを忘れていてハマった
• 計算量
  • 辺の容量が1なので計算量が良くなっていて、O(nm)で見ておけば十分 (頂点数n=500程までかな)
  • https://atcoder.github.io/ac-library/document_ja/maxflow.html

#include <atcoder/maxflow>
using namespace atcoder; // 忘れがち

// 入力：DAGなグラフG
// 出力：最小パス被覆
ll minimum_path_cover(VV& G){
  ll N = SZ(G);
  ll source = 2*N;
  ll sink = 2*N+1;
  mf_graph<ll> flow(2*N+2);

  rep(i,N){
    flow.add_edge(source,i,1);
    flow.add_edge(N+i,sink,1);
  }
  // 二重辺をはらないように注意
  rep(i,N){
    for(ll to : G[i]){
      flow.add_edge(i, to+N, 1);
    }
  }
  ll max_flow = flow.flow(source, sink);
  return N - max_flow;
}

int main(){
    cin.tie(0);
    ios::sync_with_stdio(false);

    // input
    while(true){
      ll N,M,L;
      cin>>N>>M>>L;
      debug(N,M,L);
      if(N==0) return 0;

      auto wf = WarshallFloyd(N);
      
      // edge
      rep(i,M){
        ll a,b,c;
        cin>>a>>b>>c;
        wf.register_edge2(a,b,c);
      }
      wf.calc();

      // requests
      VI P(L);
      VI T(L);
      rep(i,L){
        cin>>P[i]>>T[i];
      }

      // リクエストiの後にリクエストjを処理できるなら辺
      // これはDAG
      VV G(L);
      rep(i,L){
        rep(j,L){
          if(i==j) continue;
          // move i to j
          ll a = P[i];
          ll b = P[j];
          ll d = wf.distance(a,b);
          if(T[i]+d<=T[j]){
            G[i].push_back(j);
          }
        }
      }

      ll ans = minimum_path_cover(G);
      p(ans);
    }
   
    return 0;
}