D. Maximum Distributed Tree ～木DP 部分木のサイズ, 深さを求めるサンプル～

Quiz
- https://codeforces.com/contest/1401/problem/D
AC
- https://codeforces.com/contest/1401/submission/91696004
解法
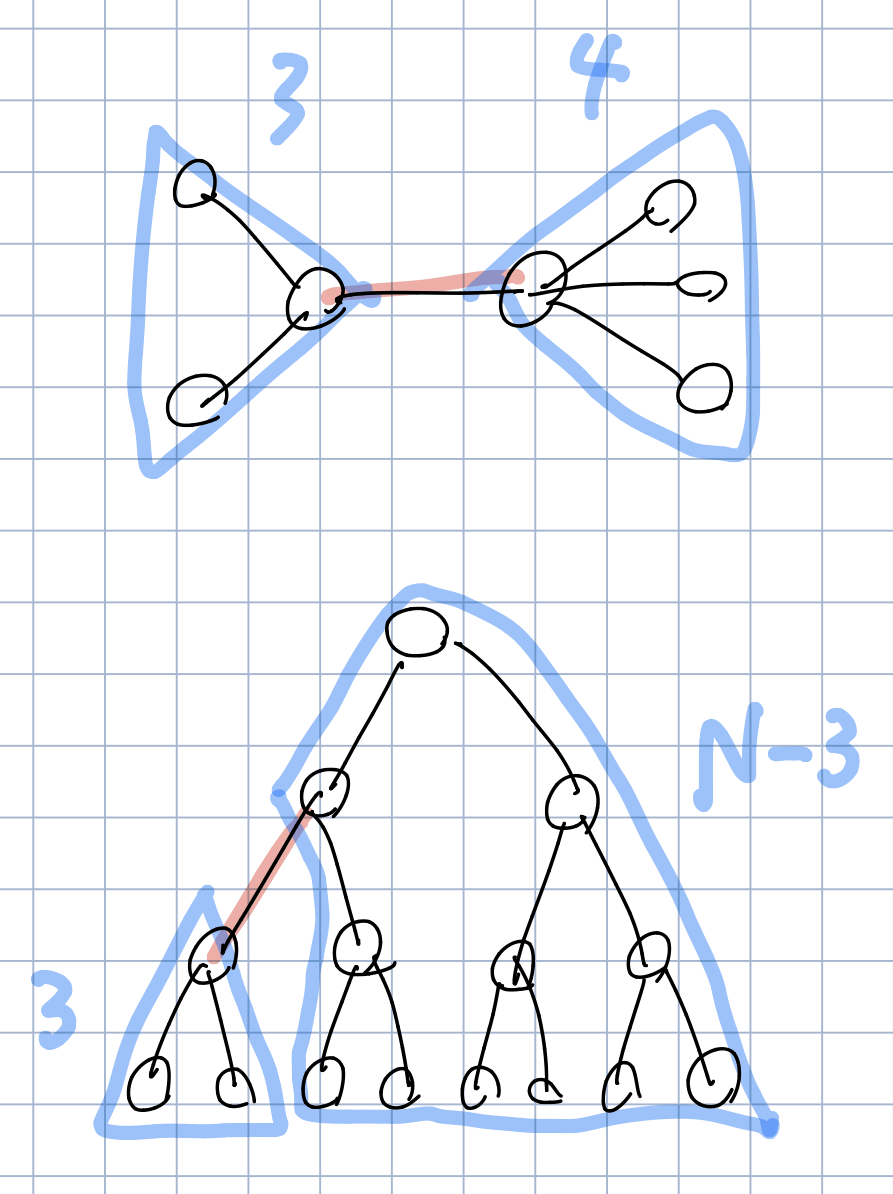
- 辺の両端のノード数の積が大きい辺に、大きい値を割り振るといい
- 木DPで根からの深さと、部分木のサイズを求めておけばいい
- 「割り振る重みが1になる辺は最小にせよ」という条件があるので、重みの個数Mが辺の本数N-1より多いかどうかで場合分けが必要。サンプルにはM<N-1の場合しかないのが不親切
私的メモ
- このコードを木DPのたたき台としよう

f:id:peroon:20200903162943p:plain

// for codeforces
void solve(){
  ll N;
  cin>>N;
  VV G(N);

  VI A(N-1);
  VI B(N-1);
  rep(i,N-1){
    ll a,b;cin>>a>>b;
    a--;b--;
    G[a].push_back(b);
    G[b].push_back(a);
    A[i]=a;
    B[i]=b;
  }

  // 深さを求めるdfs
  VI depth(N, -1);
  function<void(ll,ll,ll)> dfs_depth = [&](ll i, ll prev, ll dep){
    depth[i]=dep;
    for(ll to : G[i]){
      if(to==prev)continue;
      dfs_depth(to,i,dep+1);
    }
    return;
  };
  dfs_depth(0,-1,0);

  // 部分木のサイズを求めるdfs
  VI dp(N, -1);
  function<ll(ll,ll)> dfs = [&](ll i, ll prev){
    ll sum=1;
    for(ll to : G[i]){
      if(to==prev)continue;
      sum += dfs(to,i);
    }
    return dp[i]=sum;
  };
  dfs(0,-1);

  // 割り振る重み
  ll M;cin>>M;
  VI P(M);
  rep(i,M)cin>>P[i];
  RSORT(P);

  // 各辺の倍率
  VI C(N-1);
  rep(i,N-1){
    ll a = A[i];
    ll b = B[i];
    // aの方が根に近いとする
    if(depth[a]>depth[b]) swap(a,b);
    // 両端のnode数
    ll c = dp[b];
    ll d = N-c;
    C[i]=c*d;
  }
  RSORT(C);

  mint ans = 0;
  if(M<N-1){
    // 全ての辺に割り当てられない場合
    P.resize(N-1,1);
    rep(i,N-1){
      mint w = P[i]*C[i]%mod;
      ans += w;
    }
  }
  else{
    // 割り当てる十分なPがある
    // [0]に多くのPを割り当てる
    ll num = M-(N-1)+1;
    mint w = C[0];
    rep(i,num) w *= P[i];
    ans += w;

    // [1]以降
    FOR(i,1,N-1){
      mint w = C[i];
      w *= P[i+num-1];
      ans += w;
    }
  }
  p(ans.x);
}

int main(){
    cin.tie(0);
    ios::sync_with_stdio(false);

    // input
    ll N; 
    cin>>N;
    
    while(N--)solve();
    
    return 0;
}