LISとLCS D - トランプ挿入ソート (abc006_4)

ライブラリ

LCS (Longest Common Subsequence)

// LCSセット
const int S_LEN_MAX = 6000;
ll dp[S_LEN_MAX][S_LEN_MAX];
ll LCS(string s, string t){
    ll n = s.size();
    ll m = t.size();
    for (int i=0; i<n; ++i) {
        for (int j=0; j<m; ++j) {
            if (s[i] == t[j]) {
                dp[i+1][j+1] = dp[i][j] + 1;
            }
            else {
                dp[i+1][j+1] = max(dp[i][j+1], dp[i+1][j]);
            }
        }
    }
    return dp[n][m];
}

LCS 復元

LCS 図示

  • 上記dp_fのサンプル
abracadabra
avadakedavra
  • (答えは7)を実行したあとのdpテーブルを出力するとこうなる
0 0 0 0 0 0 0 0 0 0 0 0 0 
0 1 1 1 1 1 1 1 1 1 1 1 1
0 1 1 1 1 1 1 1 1 1 1 1 1
0 1 1 1 1 1 1 1 1 1 1 2 2 
0 1 1 2 2 2 2 2 2 2 2 2 3
0 1 1 2 2 2 2 2 2 2 2 2 3
0 1 1 2 2 3 3 3 3 3 3 3 3
0 1 1 2 3 3 3 3 4 4 4 4 4
0 1 1 2 3 4 4 4 4 5 5 5 5
0 1 1 2 3 4 4 4 4 5 5 5 5
0 1 1 2 3 4 4 4 4 5 5 6 6
0 1 1 2 3 4 4 4 4 5 5 6 7

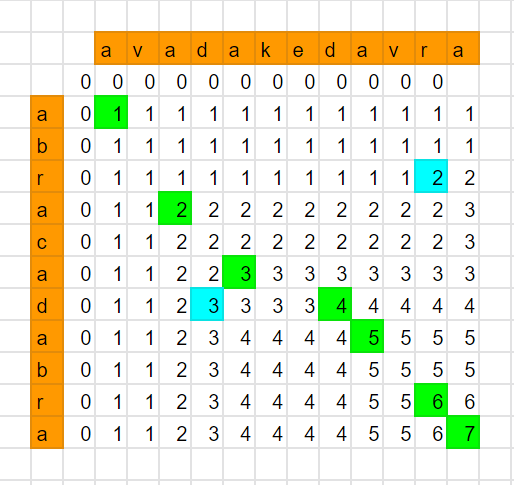
f:id:peroon:20200129065039p:plain

  • 同じ数値ごとに見て、左上が尖っているものを取ればいいように見えるが、それは少し違う
  • 画像の右上の水色を見てみると、左上が尖っているものを選んでいるが、この遷移では最終的な長さ7へは辿り着けない
  • 終端側（LCSの7）から6, 5... とたどっていく必要がある
  • 画像左下の水色は、4(緑)と同じ行を使っているのでNG
  • 辿り方の参考２

LIS (Longest Increasing Subsequence)