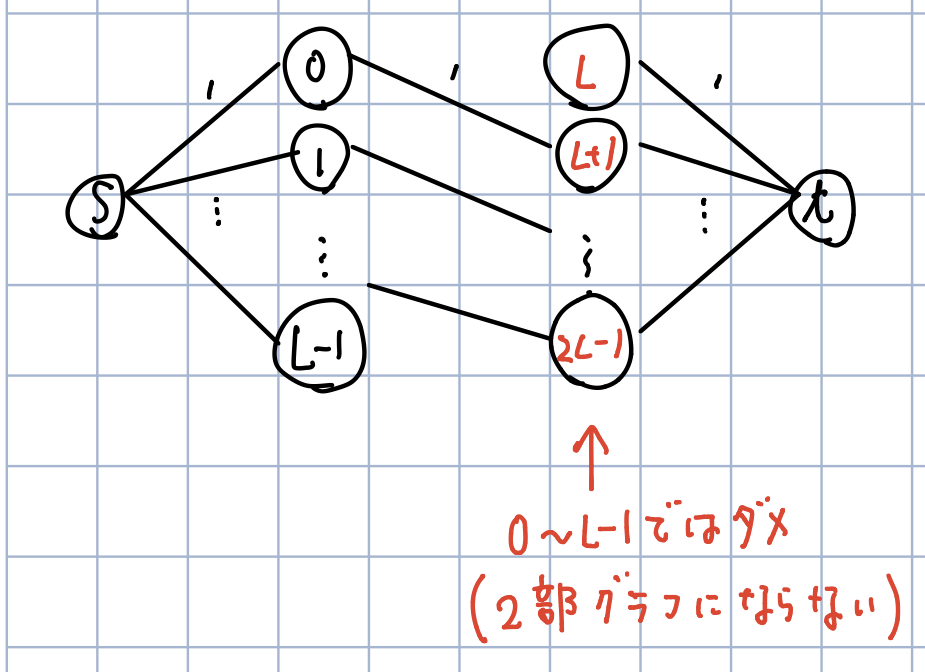
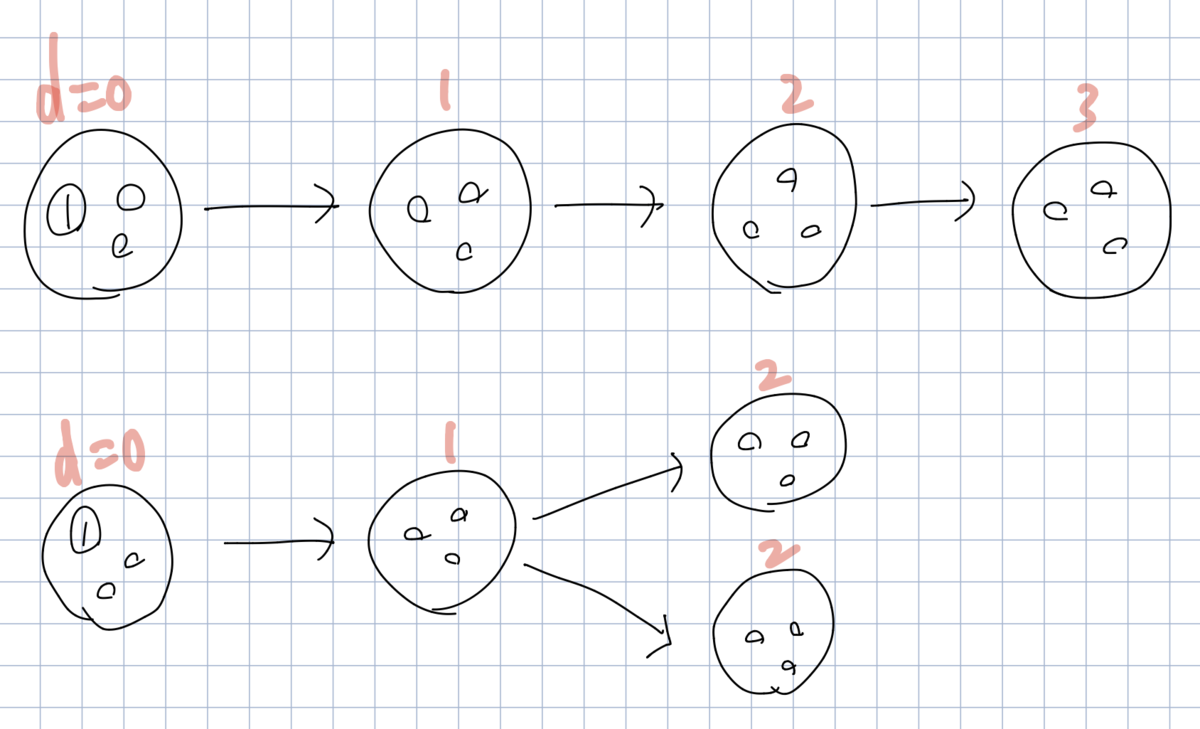
- Quiz
- AC
- 解説
- 点と直線の距離ではないので注意
- 点を線分に射影した後、射影された点が線分内にいるかもチェックした
- その他
- ライブラリとしてまあまあ整った
- ベクトルの平行判定にて、「外積=0なら平行」を使ったが、0の判定と誤差の関係でハマった。具体的にはEPSを荒くすることで通った
#define EPS (1e-12)
#define equals(a,b) (fabs((a)-(b)) < EPS)
code (library)
typedef complex<ld> C;
VI get_a_b_c_from_two_points(C p, C q){
ll x1=p.real();
ll y1=p.imag();
ll x2=q.real();
ll y2=q.imag();
ll a = y1-y2;
ll b = x2-x1;
ll c = y1*(x2-x1)-x1*(y2-y1);
return {a,b,c};
}
ld cross(C a, C b){
return a.real()*b.imag() - a.imag()*b.real();
}
ld dot(C a, C b){
return a.real() * b.real() + a.imag() * b.imag();
}
ld length(C v){
return sqrt(v.real()*v.real() + v.imag()*v.imag());
}
ld distance_between_two_points(C a, C b){
return length(a-b);
}
C unit_vector(C v){
return v / length(v);
}
C point_projection_to_line(C p, C a, C b){
C v = b-a;
C u = unit_vector(v);
C AP = p - a;
ld len = dot(AP, u);
return a + u*len;
}
bool is_same_position(C a, C b){
ld d = distance_between_two_points(a,b);
if(equals(d,0))return true;
return false;
}
bool is_parallel(C v, C w){
ld area = cross(v,w);
if(equals(area,0))return true;
return false;
}
bool is_in_segment(C p, C a, C b){
if(is_same_position(p,a))return true;
if(is_same_position(p,b))return true;
auto pa = a-p;
auto pb = b-p;
if(!is_parallel(pa,pb))return false;
if(dot(pa,pb)<0)return true;
return false;
}
ld distance_point_to_segment(C p, C a, C b){
ld mi = inf;
chmin(mi, distance_between_two_points(p,a));
chmin(mi, distance_between_two_points(p,b));
C q = point_projection_to_line(p,a,b);
if(is_in_segment(q,a,b)){
chmin(mi, distance_between_two_points(p,q));
}
return mi;
}
bool is_intersect(C p0, C p1, C q0, C q1){
{
if(p0==p1)return true;
if(p0==q0)return true;
if(p0==q1)return true;
if(p1==q0)return true;
if(p1==q1)return true;
if(q0==q1)return true;
}
bool is_parallel = false;
{
C v = p0-p1;
C w = q0-q1;
if(cross(v,w)==0) is_parallel=true;
}
if(is_parallel){
if(is_in_segment(p0,q0,q1))return true;
if(is_in_segment(p1,q0,q1))return true;
if(is_in_segment(q0,p0,p1))return true;
if(is_in_segment(q1,p0,p1))return true;
return false;
}
auto v0 = p1 - p0;
auto v1 = q0 - p0;
auto v2 = q1 - p0;
if(cross(v0, v1) * cross(v0, v2) > 0){
return false;
}
v0 = q1 - q0;
v1 = p0 - q0;
v2 = p1 - q0;
if(cross(v0, v1) * cross(v0, v2) > 0){
return false;
}
return true;
}
他人のライブラリ
verify